The application of Optimisation and Bayesian inference on experimental cyclic voltammograms has been successful in quantifing the parameters involved in cyclic voltammetry since Gavaghan (2018). BIOMEC incorporates these techniques with the Monash Electro-chemical Simulator (MECSim) allowing the same computational optimisation and Markov Chain Monte Carlo method based Bayesian inference calculations on experimental data for a wide range of reaction mechanisms.

First published in Gundry (2021) BIOMEC incorporates and expands a range of noise models for the optimisation of DC and Fourier Transformed AC voltammetry experimental data. This process is completed by iteratively comparing the experimental datas current trace to simulated reaction models. The package can be found and downloaded on the public GITHUB repository and requires singularity to run on UNIX based systems. Though being highly paralyzable and scalable to many parameters the computational optimisations generally take between five minutes to one hours. With the Bayesian inference calculations taking anywhere between 4 to 48 hours depending on the reaction mechanism complexity. Due to this and the complexity of the input files for setting up these more quantitative calculation methods are difficult for web based integration. As such, cloud based method of running these methods on experimental data is still in production.

If you are interested in running these algorithms on your data yourself. It is recommended to download the source code from the above GITHUB repo and setting up the BIOMEC container to run on a local machine yourself. In that case the following Youtube videos have information for the algorithms used, the process of installing the singularity program and setting up the input files for analysis of experimental data.

Example results

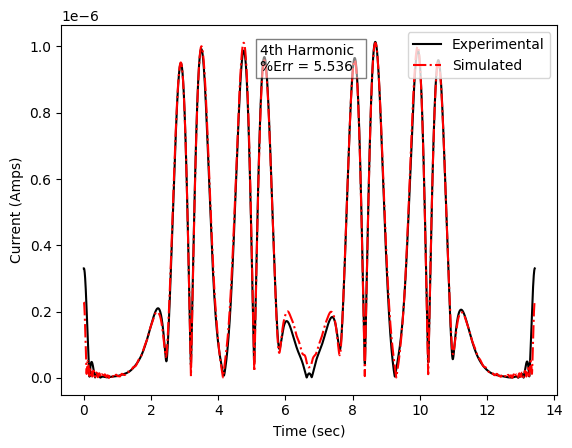
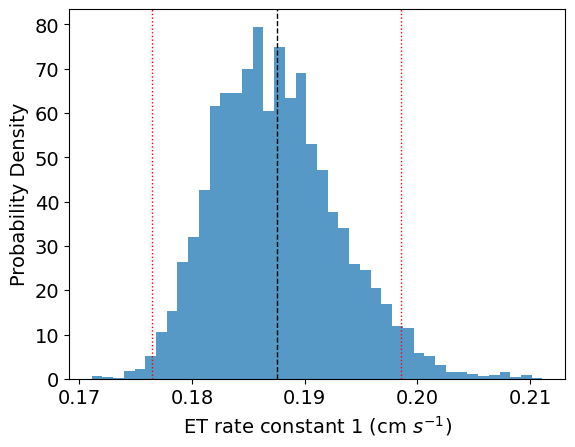
Example of an automated fit to experimental data for a MCMC Bayesian inference calculation for a two single electron transfer redox system. (Left) is the fifth harmonic of an experimental data compared to the simulated best fit calculated from the Bayesian inference algorithm, (Right) is the posterior distribution (the uncertainty of a specific parameter) for the first electron transfer rate given the fit of the simulation to experimental data.